[1]许文彬.一类变指数退化抛物方程的解[J].集美大学学报(自然科学版),2021,26(6):0-0.
XU Wenbin.Solutions of a Kind of Degenerate Parabolic Equation with Variable Exponent[J].Journal of Jimei University,2021,26(6):0-0.
点击复制
一类变指数退化抛物方程的解(PDF)
XU Wenbin.Solutions of a Kind of Degenerate Parabolic Equation with Variable Exponent[J].Journal of Jimei University,2021,26(6):0-0.
《集美大学学报(自然科学版)》[ISSN:1007-7405/CN:35-1186/N]
- 卷:
- 第26卷
- 期数:
- 2021年第6期
- 页码:
- 0-0
- 栏目:
- 数理科学与信息工程
- 出版日期:
- 2021-12-28
文章信息/Info
- Title:
- Solutions of a Kind of Degenerate Parabolic Equation with Variable Exponent
- 作者:
- 许文彬
- (集美大学理学院,福建 厦门 361021)
- Author(s):
- XU Wenbin
- (School of ScienceJimei UniversityXiamen 361021China)
- 分类号:
- -
- DOI:
- -
- 文献标志码:
- -
- 摘要:
-
考虑如下的变指数退化抛物方程
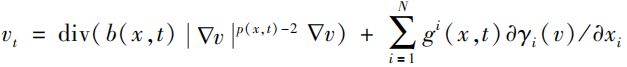 解的适定性问题。利用抛物正则化方法证明了解的存在性。对检验函数适当选取,证明了解的唯一性。在边界
解的适定性问题。利用抛物正则化方法证明了解的存在性。对检验函数适当选取,证明了解的唯一性。在边界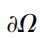 上,扩散系数b(x,t)=0,解的唯一性可以不依赖于边界条件。
上,扩散系数b(x,t)=0,解的唯一性可以不依赖于边界条件。
- Abstract:
-
The wellposedness problem of a kind of degenerate parabolic equation
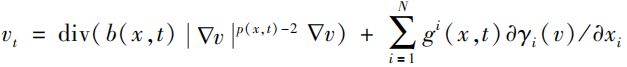 were considered.By a parabolically regularized method,the existence of weak solutions was proved.By choosing a suitable test function,the uniqueness of weak solution was also proved.The diffusion
were considered.By a parabolically regularized method,the existence of weak solutions was proved.By choosing a suitable test function,the uniqueness of weak solution was also proved.The diffusion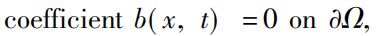 ,the uniqueness theory could be established which was independent of the boundary value condition.
,the uniqueness theory could be established which was independent of the boundary value condition.
参考文献/References:
-
相似文献/References:
[1]方聪娜,王全义,谢惠琴,等.具有有限时滞中立型泛函微分方程的概周期解[J].集美大学学报(自然科学版),2010,15(6):71.[doi:2010/12/30 0:00:00]
[2]方聪娜,王全义,谢惠琴.具有有限时滞中立型泛函微分方程的概周期解[J].集美大学学报(自然科学版),2010,15(6):471.
[3]谢清梅,詹华税.带有吸附项的边界扩散退化抛物方程解的性质[J].集美大学学报(自然科学版),2012,17(1):71.
XIE Qing-meiZHAN Hua-shui.Properties of the Boundary Degenerate ParabolicEquation with Adsorption Item[J].Journal of Jimei University,2012,17(6):71.
[4]叶霞,黄志圣,黄臻鑫,等.二维定常的微流边界层解的存在性[J].集美大学学报(自然科学版),2012,17(3):217.
[5]黄志圣,叶霞,詹华税.对称定常微流边界层[J].集美大学学报(自然科学版),2013,18(1):54.
HUANG Zhi-sheng,YE Xia,ZHAN Hua-shui.Axially Symmetric Stationary Micro-fluid Boundary Layer[J].Journal of Jimei University,2013,18(6):54.
[6]汤林冰,詹华税.一类抛物型偏微分方程的W1.12弱解存在性[J].集美大学学报(自然科学版),2013,18(5):373.
TANG Lin-bing,ZHAN Hua-shui.W1.12-Weak Solution Existence About Some Parabolic Equation[J].Journal of Jimei University,2013,18(6):373.
备注/Memo
- 备注/Memo:
- -

